Machine Learning Garden
Powered by 🌱Roam GardenSoftmax
References
Notes {{word-count}}
Summary:
Key points:
How to make a number postive?
is especially convenient because it is one to one and onto and it maps the entire real number line to an entire set of positive real numbers.
How to make a bunch of numbers sum to 1?
We do this using normalization by .
For possible labels, is a vector of elements, and is a vector -valued function with outputs.
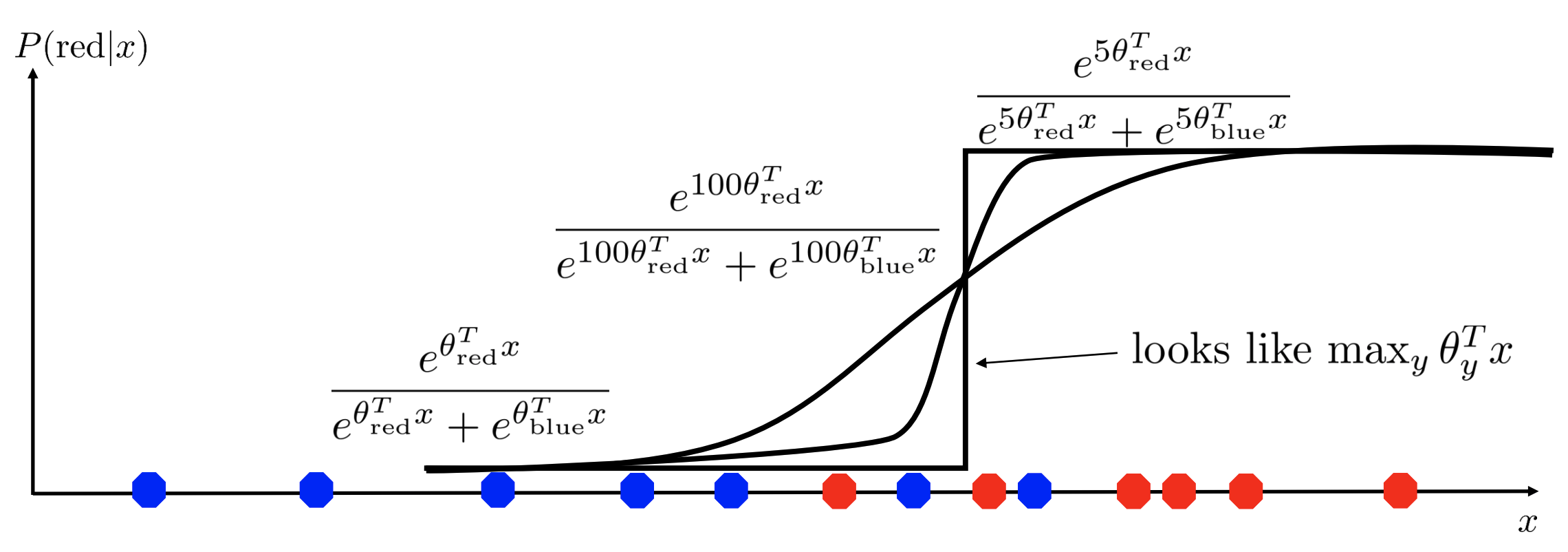
Why is it called a Softmax?